Bilangan kompleks adalah kumpulan titik yang dibentuk oleh bilangan nyata dan bilangan khayal, dalam bilangan kompleks. Bilangan kompleks dalam teknik listrik digunakan untuk menggambarkan sifat arus listrik bolak-balik. Suatu bilangan kompleks dapat ditulis dalam bentuk :
W = a + jb
Keterangan :W = Bilangan Kompleks
a dan b = Bilangan nyata (bilangan real) : Bilangan nyata atau bilangan real dalam matematika adalah suatu bilangan yang dapat ditulis dalam bentuk desimal. Bilangan nyata meliputi bilangan rasional dan bilangan irasional.
j = Bilangan khayal (bilangan imaginar) : Bilangan khayal atau bilangan imaginar adalah bilangan yang memiliki sifat i2 = -1. Bilangan i diperoleh dari penyelesaian persamaan kuadratik :
x2 + 1 = 0atau secara ekuivalen :
x2 = -1
atau juga sering dituliskan sebagai
x = √-1
Dalam bilangan kompleks ada lima jenis operasi yang sering digunakan, yaitu kesamaan, penjumlahan, pengurangan, perkalian, dan pembagian.
Misal diketahui dua bilangan kompleks yaitu :P = a + jb
Q = c + jd
a. Persamaan : dua bilangan kompleks adalah sama jika dan hanya bilangan nyata bilangan khayal sama.
P = Q bila a = b dan c = d
b. Penjumlahan : Penjumlahan dua buah bilangan kompleks adalah dengan menjumlahkan masing-masing bilangan nyata dan bilangan khayal.
P + Q = ( a + c ) + j ( c - d )
c. Pengurangan : Pengurangan dua bilangan kompleks adalah dengan mengurangkan masing-masing bilangan nyata dan bilangan khayal.
P - Q = ( a - c ) + j ( c + d )
d. Perkalian : Perkalian dua bilangan kompleks dilakukan seperti parkalian aljabar biasa, kemudian hasil kali yang sejenis dijumlahkan.
P . Q = ( a + jb ) . ( C + jd)= ac + j2bd + jbc + jad
= ( ac - bd ) + j ( bc + ad )
e. Pembagian : Pembagian dua buah bilangan kompleks dilakukan dengan menggunakan kompleks sekawan dari pembagi dengan kata lain bilangan khayal pada pembagi usaha hilang.
Bilangan kompleks juga memiliki besaran dan arah sudut :
W = a + jb
= M.cos θ + jM.sin θ
= M (cos θ + j sin θ)
keterangan :
M = modulus harga sebenarnya bilangan kompleks
θ = sudut arah dari bilangan kompleks
Bila bilangan kompleks dituliskan dalam bilangan polar menjadi :
W = a + jb
= M (cos θ + j sin θ)
= M ∠ θ
keterangan :
M = √a2 + b2
θ = arc tg b/a
Untuk penulisan dengan bilangan eksponensial menggunakan dasar theorema Euler.
ejθ = cos θ + sin θ
Jadi persamaan eksponensial menjadi :
W = a + bj
= M.(cos θ + j sin θ)
= M ∠ θ
= M . ejθ
Contoh soal :
1. Suatu beban pada rangkaian listrik memiliki nilai impedansi yang dituliskan dengan bilangan kompleks Z = (5 + j4)Ω, berapakah nilai impedansi jika dituliskan dalam bentuk polar?
Jawab:
2. Diketahui 2 buah besaran dituliskan dengan menggunakan bilangan kompleks yaitu A = (4 + j5)Ω dan B = (3 - j2)Ω. maka berapakah hasil dari A + B, A - B, A . B, dan A/B ?
Jawab :
a. A + B :
b. A - B :
c. A . B :
d. A/B :
Jawab :
a. A + B :
b. A - B :
d. A/B :






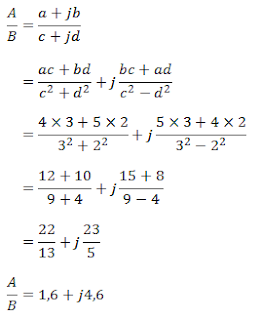
0 Komentar:
Posting Komentar