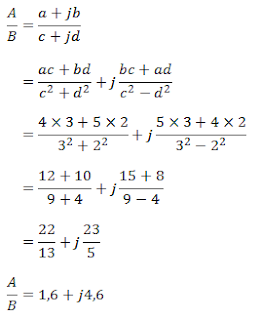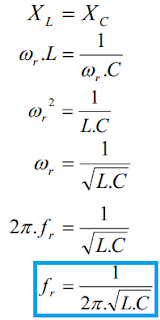Impedansi dengan bilangan Kompleks

Bilangan kompleks adalah suatu bilangan yang terbentuk dari bilangan nyata dan bilangan khayal. Impedansi (Z)dapat dituliskan dengan bilangan kompleks. Bilangan nyata digunakan untuk menyatakan nilai komponen Resistor yang memiliki beda fasa yang besarnya 0^o. Bilangan khayal digunakan untuk menyatakan nilai reaktansi (X). Reaktansi induktif (X_L) dinyatakan sebagai +j jika beban digunakan adalah komponen berupa induktor, yang memiliki besar sudut 90^o. Reaktansi kapasitif (X_C) dinyatakan -j jika beban yang digunakan adalah komponen berupa kapasitor yang memiliki nilai sudut -90^o.

Persamaan Impedansi dengan bilangan kompleks :

Keterangan :
Z = Impedansi (Ω)
R = Baban resistansi (Resistor) bilangan nyata (Ω)
X = Reaktansi (Ω)
jXL atau jXC = beban reaktansi (L = Induktor, C = Kapasitor) bilangan khayal (Ω)

Contoh soal :

1. Dua buah impedansi dihubungkan dengan sumber tegangan bolak-balik yang memiliki nilai masing-masing  Z1 = (2 + j4)Ω  dan  Z2 = (4 - j12)Ω.

a. Berapakah nilai masing-masing impedansi jika ditulis dalam bentuk polar?
b. Berapakah nilai Impedansi total jika kedua impedansi tersebut dirangkai secara seri?
c. Berapakah nilai Impedansi total jika kedua impedansi tersebut dirangkai secara paralel?

Diketahui :
Z1 = (2 + j4)Ω
Z2 = (4 - j12)Ω

Jawab :
a. Nilai masing-masing impedansi dalam bentuk polar :

b. Nilai impedansi yang dirangakai secara seri :

c. Nilai impedansi yang dirangkai secara paralel :

Rangkaian Segitiga (Δ)

Gambar rangkaian beban Segitiga (Δ)

Rangkaian segitiga (Δ) ujung-ujung beban dihubungkan saling menyilang antara satu dengan lainnya. Terminal U1 dan W2 disatukan dengan sumber dari fasa L1. U2 dan V1 disatukan dengan sumber dari fasa L2. V2 dan W1 disatukan dengan fasa L3. Masing-masing sumber dirangkai dengan sebuah amper meter untuk mengukur besar nilai arus I₁, I₂, dan I₃:

I₁ = I₁₂ - I₃₁
I₂ = I₂₃ - I₁₂
I₃ = I₃₁ - I₃₂

Rangkaian segitiga tidak ada memiliki nilai tegangan fasa-netral, pada rangkaian segitiga hanya memiliki nilai tegangan fasa-fasa atau tegangan antar fasa. Persamaan arus listrik dan tegangan listrik pada rangkaian segitiga :

Keterangan :
I    = Arus listrik (A)
I_str = Arus listrik start (A)
V   = Tegangan listrik (V)
V_str= Tegangan listrik start (V)

Rangkaian segitiga pada terminal motor listrik 3 fasa :

Pada terminal box motor 3 fasa memiliki notasi 2 macam notasi standar. Notasi yang pertama terdiri dari ujung lilitan fasa (W2, U2, dan V2) dan (U1, V1, dan W1). Notasi yang kedua terdiri dari ujung lilitan fasa (Z, X, dan Y) dan (U, V, dan W). Ketika dituliskan pada motor induksi 3 fasa :

Gambar rangkaian segitiga pada motor listrik 3 fasa

Keterangan :
U1 = U   |   W2= Z   |   L1 = R
V1 = V   |   U2 = X   |   L2 = S
W1= W  |   V2 = Y   |   L3 = T

Pada rangkaian segitiga terminal W2 dan U1 dirangkai menjadi satu, U2 dan V1 dirangkai menjadi satu, V2 dan W1 dirangkai menjadi satu (seperti pada gambar dihubungkan dengan garis berwarna merah jambu). Terminal V1 dihubungkan dengan L1, Terminal V1 dihubungkan dengan L2, dan terminal W1 dihubungkan dengan L3.

Rangkaian Bintang (Y)

Rangkaian bintang (Y) adalah rangkaian beban listrik 3 fasa yang bentuk huruf Y. Rangkaian segitiga (Δ) adalah rangkaian beban listrik 3 fasa yang berbentuk segitiga. Untuk membedakan rangkaian bintang dan rangkaian segitiga yaitu dengan mengetahui rangkaian bintang terdapat tegangan fasa-netral V_1N, V_2N, dan V_3N. Selain itu juga memiliki nilai tegangan fasa-fasa atau tegangan antar fasa V₁₂, V₂₃, dan V₃₁. Sedangkan pada rangkaian segitiga hanya terdapat tegangan antara fasa nya saja.

Gambar tegangan bintang dan segitiga

Analisa secara grafis dapat dijelaskan sebagai berikut :

Keterangan :

V₃₁ = Tegangan fasa 3 ke fasa 1

V_1N = Tegangan fasa 1 ke netral

√3   = Faktor pengendali

Gambar rangkaian beban bintang (Y)

Rangkaian bintang (Y) adalah rangkaian beban listrik yang memiliki nilai tegangan fasa-netral dan tegangan antar fasa. Rangkaian bintang miliki nilai tegangan fasa-netral V_1N, V_2N, dan V_3N. Selain tegangan memiliki nilai tegangan fasa-netral juga memiliki nilai tegangan fasa-fasa atau tegangan antar fasa V₁₂, V₂₃, dan V₃₁.

Grafik tegangan fasa-netral dan tegangan antar fasa. Tegangan fasa V_1N bergerak dari sudut 0^o sampai dengan 360^o. Tegangan fasa V_3N bergerak dari 60^o sampai 420^o. Tegangan antar fasa V₁₃ merupakan penjumlahan vektor (V_1N + V_3N) bergerak dari 30^o, sampai dengan 390^o.

Gambar tegangan fasa netral, tegangan fasa ke fasa

Nilai tegangan antar fasa V₁₂, V₂₃, V₃₁ = 380 V, sedangkan nilai tegangan fasa-netral V_1N, V_2N, V_3N = 220 V.

Gambar pengukuran tegangan antar fasa dan tegangan fasa-netral

Beban hubungan bintang terminal U2, V2, dan W2 disatukan. jala-jala L1-U1, L2V1, dan L3-W1. Dirangkai dengan empat buah amper meter yang digunakan untuk mengukur nilai I₁, I₂, I₃ dan I_N. Ketika beban seimbang I₁ = I₂ = I₃ ampere I_N = 0. Tegangan fasa V₁₂, V₂₃, V₃₁ besarnya 380V, maka tegangan fasa-netral V_1N, V_2N, V_3N besarnya :

Keterangan :
V    = Tegangan listrik (V)
V_str = Tegangan listrik start (V)
I    = Arus listrik (A)
I_str = Arus listrik strat (A)

Bentuk gelombang arus listrik 3 fasa I₁ berawal dari  0^o, 180^o dan berakhir di sudut α 360^o. Arus I₂ berawl dari 120^o, 300^o dan berakhir di sudut α 480^o. Arus I₃ berawal dari 240^o dan berakhir di sudut α 600^o. Antara I₁, I₂, I₃ masing-masing berbeda 120^o.

Gambar gelombang sinus 3 fasa

Rangkaian diagram vektor tegangan, dirangkai dengan tiga buah beban resistor yang besarnya identik sama, terhubung secara bintang. Vektor tegangan V_1N, V_2N dan V_3N. masing-masing beban sudut 120^o. Besar tegangan dan arus I₁ akan se-fasa dengan V_1N,  dan vektor I₂ akan se-fasa dengan V_2N dan I₃ sefasa dengan V_3N. kondisi ini sering disebut dengan seimbang.

Gambar diagram vektor tegangan dan Arus 3 fasa dengan beban seimbang

Beban pada Rangkaian Bintang (Y) yang Tidak Seimbang

3 beban resistor yang yang memiliki nilai tidak sama dirangkai secara bintang (Y). penunjuk pada ampermeter I₁ = 2,5A; I₂ = 2,0A; I₃ = 1,0A; dan I_N = 1,2A.

Gambar vektor tegangan dan arus beban resistif tidak seimbang dengan sekala 1cm = 1A

Beban tidak seimbang mengakibatkan ada arus yang mengalir melalui kawat netral, sebesar I_N = 1,2A. akibat lainnya tegangan fasa-netral V_1N, V_2N, dan V_3N juga berubah, posisi titik netral N bergeser kearah kiri bawah N. V₁₂, V₂₃, dan V₃₁ tetap simetris. oleh sebab itu pada pada rangkaian bintang beban tiap fasa harus seimbang, sehingga tidak mengganggu tegangan fasa-netral.

Gambar vektor tegangan fasa-netral, beban tidak seimbang

Rangkaian bintang (Y) pada terminal motor listrik 3 fasa :

Pada terminal box motor induksi 3 fasa memiliki notasi standar. Urutan ujung lilitan fasa W2, U2, dan V2 dan pada ujung lilitan yang lainnya diberikan notasi U1, V1, dan W1. Ada pula cara lain menuliskan notasi pada motor induksi 3 fasa yaitu :

Gambar rangkaian bintang pada motor listrik 3 fasa

Keterangan :

U1  = U

V1  = V

W1 = W

W2 = Z

U2  = X

V2  = Y

L1  = R

L2  = S

L3  = T

Rangkaian bintang, terminal W2, U2, V3 dirangkai menjadi satu sebagai titik bintang (pada gambar dihubungkan dengan garis berwarna pink). Terminal U1 dihubungkan dengan L1, terminal V1 dihubungkan dengan L2, dan terminal W1 dihubungkan dengan L3.

Generator Listrik 3 Fasa

Gambar prinsip tangan Kanan Flamming

Prinsip dasar pembangkitan listrik berdasarkan hukum tangan kanan Flaming. Penghantar berada di telapak tangan kanan yang membuka, ditembus oleh medan magnet Φ dari kutub magnet utara-selatan, kawat digerakkan ke arah ibu jari, maka akan timbul arus listrik yang searah dengan keempat jari. 

Gambar pembangkit tegangan induksi

Sebatang logam di kedua ujung digantung dengan kawat fleksibel, ditempatkan diantara dua kutub magnet utara-selatan. Kawat diarahkan searah anak panah, keluar masuk, sehingga batang kawat dipotong oleh fluk magnet. Di ujung penghantar dipasang pengukur tegangan listrik, jarum penunjuk pada volt meter akan menunjuk ke kanan dan ke kiri. Prinsip ini dasar pembangkitan listrik AC. Rumus untuk menghitung tegangan induksi :

Keterangan :

vi = Tegangan Induksi (V)

B = Fluk magnet

I = Panjang penghantar (m)

v = Kecepatan rata-rata (m/s)

Z = Jumlah pengahantar

Gambar generator 3 fasa

Generator adalah alat yang mengubah energi mekanik menjadi energi mekanik (gerak) menjadi energi listrik. Konstruksi generator tiga fasa terdiri dari stator dan rotor. Stator adalah bagian generator yang diam, diantaranya badan generator, lilitan stator, sikat arang, terminal box.
Rotor merupakan bagian generator yang bergerak, terdiri dari kutub rotor, slipring. lilitan stator terdiri dari 3 fasa yaitu lilitan fasa U, lilitan phasa V dan lilitan fasa . Ujung-ujung lilitan diberikan notasi U1-U2, V1-V2, dan W1-W2.
Rotor memiliki dua kutub utara (N) north, dan kutub selatan (S) south. Arus listrik DC yang mengalir melewati slipring dan sikat arang, tujuannya untuk mendapatkan fluk magnet yang diatur besarnya. Aliran listrik dari pembangkit, pengukuran tegangan dan penyaluran daya ke beban 3 fasa, dalam hubungan bintang (Y) dan segitiga (Δ).

Gambar rangkaian pembangkit, pengukuran dan beban bintang segitiga

Listrik 3 fasa dari pembangkit, fasa U, V dan W, tegangan ketiga fasa masing-masing berbeda 120^o. fasa U mengalirkan arus I₁, fasa V mengalirkan arus listrik I₂ dan phasa W mengaliarkan arus I₃. dengan jala-jala L1, L2, L3, dan N tegangan diukur dengan tiga buah voltmeter. Tegangan L1-L2 terukur V₁₂, tegangan L2-L3 terukur V₂₃ dan tegangan L3-L1 terukur V₃₁.

Aliran ke beban ada dua jenis, beban bintang (Y) dan beban segitiga (Δ). Beban bintang mengunakan empat kawat L1-U, L2-V, L2-W dan N-N. Lilitan beban mendapatkan arus fasa, juga mendapatkan tegangan fasa-netral. Rumus tegangan fasa-fasa :

Pada beban segitiga, dipakai tiga penghantar jala-jala ke beban dengan hubungan L1-U1W2, L2-U2V1, dan L3-V2W1. Setiap lilitan mendapatkan tegangan phasa-phsa V12, V 23, dan V31, demikian juga dengan arus jala-jala I12, I23, dan I31. Rumus Arus jala-jala :

Bilangan Kompleks

Bilangan kompleks adalah kumpulan titik yang dibentuk oleh bilangan nyata dan bilangan khayal, dalam bilangan kompleks. Bilangan kompleks dalam teknik listrik digunakan untuk menggambarkan sifat arus listrik bolak-balik. Suatu bilangan kompleks dapat ditulis dalam bentuk :

W = a + jb

Keterangan :
W = Bilangan Kompleks

a dan b = Bilangan nyata (bilangan real) : Bilangan nyata atau bilangan real dalam matematika adalah suatu bilangan yang dapat ditulis dalam bentuk desimal. Bilangan nyata meliputi bilangan rasional dan bilangan irasional.

j = Bilangan khayal (bilangan imaginar) : Bilangan khayal atau bilangan imaginar adalah bilangan yang memiliki sifat i² = -1. Bilangan i diperoleh dari penyelesaian persamaan kuadratik :

x² + 1 = 0
atau secara ekuivalen :
x² = -1
atau juga sering dituliskan  sebagai
x = √-1

Dalam bilangan kompleks ada lima jenis operasi yang sering digunakan, yaitu kesamaan, penjumlahan, pengurangan, perkalian, dan pembagian.

Misal diketahui dua bilangan kompleks yaitu :
P = a + jb
Q = c + jd

a. Persamaan : dua bilangan kompleks adalah sama jika dan hanya bilangan nyata bilangan khayal sama.

P = Q     bila    a = b    dan    c = d

b. Penjumlahan : Penjumlahan dua buah bilangan kompleks adalah dengan menjumlahkan masing-masing bilangan nyata dan bilangan khayal.

P + Q = ( a + c ) + j ( c - d )

c. Pengurangan  : Pengurangan dua bilangan kompleks adalah dengan mengurangkan masing-masing bilangan nyata dan bilangan khayal.

P - Q = ( a - c ) + j ( c + d )

d. Perkalian : Perkalian dua bilangan kompleks dilakukan seperti parkalian aljabar biasa, kemudian hasil kali yang sejenis dijumlahkan.

P . Q  = ( a + jb ) . ( C + jd)
          = ac + j²bd + jbc + jad
          = ( ac - bd ) + j ( bc + ad )

e. Pembagian : Pembagian dua buah bilangan kompleks dilakukan dengan menggunakan kompleks sekawan dari pembagi dengan kata lain bilangan khayal pada pembagi usaha hilang.

Bilangan kompleks juga memiliki besaran dan arah sudut :
W = a + jb
     = M.cos θ + jM.sin θ
     = M (cos θ + j sin θ)

keterangan :
M = modulus harga sebenarnya bilangan kompleks
θ = sudut arah dari bilangan kompleks

Bila bilangan kompleks dituliskan dalam bilangan polar menjadi :
W = a  + jb
     = M (cos θ + j sin θ)
     = M ∠ θ

keterangan :
M = √a² + b²
θ = arc tg ^b/_a

Untuk penulisan dengan bilangan eksponensial menggunakan dasar theorema Euler.
e^jθ = cos θ + sin θ

Jadi persamaan eksponensial menjadi :
W = a + bj
     = M.(cos θ + j sin θ)
     = M ∠ θ
     = M . e^jθ

Contoh soal :

1. Suatu beban pada rangkaian listrik memiliki nilai impedansi yang dituliskan dengan bilangan kompleks Z = (5 + j4)Ω, berapakah nilai impedansi jika dituliskan dalam bentuk polar? 

Jawab:

2. Diketahui 2 buah besaran dituliskan dengan menggunakan bilangan kompleks yaitu A = (4 + j5)Ω dan B = (3 - j2)Ω. maka berapakah hasil dari A + B, A - B, A . B, dan A/B ?

Jawab :
a. A + B :

b. A - B :

c. A . B :

d. A/B :

Resonansi Listrik

Resonansi adalah kondisi ketika dua frekuensi yang sama saling bergetar. sebuah induktor yang terdiri dari 600 lilit kawat pada inti U-I, diragkai dengan kapasitor dengan nilai kapasitas 8,2 μF. dihubungkan dengan sumber tegangan 25 V frekuensi 50 Hz. Dengan menggeser kan inti besi I ke kiri-kanan, terjadi perubahan penunjukan arus A, tegangan V_BL dan V_BC. ketika tegangan V_BL = V_BC, terjadi penunjukan arus maksimum, saat itulah terjadi resonansi.

Gambar vektor diagram arus

Rangkaian resonansi seri resistor, induktor dan kapasitor akan terjadi tiga kemungkinan :

1. Ketika kondisi reaktansi X_L < X_C, yang terjadi tegangan V_BC > V_BL, maka rangkaian akan bersifat kapasitif.

2. Ketika kondisi reaktansi X_L = X_C, yang terjadi tegangan V_BC = V_BC. Ampermeter akan menunjukan arus maksimum, maka beban akan bersifat resistif.

3. Ketika kondisi reaktansi X_L > X_C, yang terjadi tegangan V_BC < V_BL, maka beban akan bersifat induktif.

Grafik arus berbentuk puncak saat terjadi frekuensi resonansi di titik F_r. Impedansi berbentuk lengkung kebawah, harga minimum terjadi di titik frekuensi resonansi (F_r).

Gambar grafik arus saat resonansi pada rangkaian R,L,C seri

Rangkaian resonansi paralel resistor, induktor dan kapasitor terjadi tiga kondisi yaitu:

1. Kondisi dimana reaktansi X_C > X_L, arus cabang I_BL > I_BC, rangkaian akan bersifat induktif.

2. Ketika resistansi X_L = X_C, arus cabang I_BL = I_BC, beban pada rangkaian bersifat resistif (menghambat).

3. Ketika resistansi X_L > X_C, arus cabang I_BC > I_BL, rangkaian akan bersifat kapasitif.

Grafik impedansi (Z) berbentuk puncak saat terjadi frekuensi resonansi di titik Fr. Arus total (I) berbentuk lengkung, harga  minimum terjadi di titik frekuensi resonansi (Fr)

 

Gambar grafik saat resonansi pada rangkaian R, L, C paralel

Persamaan frekuensi resonansi :

Keterangan :
ƒ_r = frekuensi resonansi (Hz)
π = 22/7 atau 3,14
L = Induktor (H)
C = Kapatias (F)
X_L = reaktansi induktif (Ω)
X_C = reaktansi kapasitif (Ω)

Contoh soal :
Jika diketahui sebuah induktor memiliki nilai 1 H di rangkai secara paralel dengan kapasitor C = 22 nF. Berapakah besar nilai frekuensi resonansi nya?

Diketahui : L = 1 H
                   C = 22 nF = 22 x 10_-9 F
Ditanya    : ƒ_r = ?
Jawab       :

Segitiga Tegangan

Gambar segitiga tegangan

Tegangan V_W, V_BL dan V membentuk sebuah segitiga dengan sudut φ antara tegangan V_w dan V. Beban dengan induktor yang berupa reaktansi induktif (X_L) di seri dengan resistor (R).bila dialiri arus bolak-balik maka akan terjadi drop tegangan V_BL pada induktor dan V_W pada resistor. Tegangan V merupakan penjumlahan secara vektor tengangan V_W dan V_BL.

Tegangan V_W se-fasa dengan arus listrik I, artinya setiap beban resistor memiliki sifat se-fasa antara tegangan dengan arus yang mengalir. Sudut fasa φ merupakan beda antara tegangan V dengan arus I, selanjutnya dapat dilanjutkan dengan menghitung nilai faktor kerja atau faktor daya cos φ.

Beban induktor berupa reaktansi kapasitirf X_L dan Resistor R dapat membentuk segitiga. Komponen R digambarkan secara horizontal, induktor X_L berbeda 90^o dari reistor. dan hasilnya adalah impedansi Z.

A. Contoh cara menggambar segitiga tegangan :
Langkah-langkah menggambar segitiga tegangan pada rangkaian resistor dirangkai secara seri dengan induktor pada sumber listrik bolak-balik sebagai berikut :

1. Membuat sekala tegangan dan arus listrik. Contoh :
skala tegangan  4 V = 1 cm,
skala arus 5 mA = 1 cm

2. Menggambar garis lurus horizontal arus listrik (I) sebagai referensi. Contoh :

3. Menggambar garis drop tegangan resistor (V_W) sejajar dengan garis arus listrik (I) dikarenakan tegangan pada resistor (R)se-fasa dengan arus listrik yang mengalir. Contoh :

4. Menggambar garis lurus vertikal drop tegangan induktor V_BL yang memiliki panjang sama dengan garis V_W dan berpangkal dengan pangkal garis V_W, sehingga antara garis V_BL dan V_W membentuk sudut 90^o. hal tersebut disebabkan oleh drop tegangan pada induktor berbeda sudut fasa sebesar 90^o  (leading) mendahului terhadap arus listrik yang mengalir atau drop tegangan pada resistor V_W. Contoh :

5. Menggambar garis yang sejajar dengan V_BL dari ujung garis V_W. Contoh :

6. Menggambar  garis miring antara titik 0 ke ujung garis sejajar V_BL, sebagai resultan tegangan V_W dan V_BL. Contoh :

B. Rumus untuk menghitung sudut pada gambar segitiga tegangan sesuai dengan gambar dibawah ini :

Rumus untuk menentukan ukuran sudut (90^o - φ):

Keterangan :

δ= Ukuran sudut (90^o - φ)

V_W = Tegangan drop pada resistor (V)

V_BL = Tegangan drop pada induktor (V)

R = Nilai resistansi pada resistor (Ω)

X_L = Nilai reaktansi kapasitif pada induktor (Ω)

Rumus ratio :

Keterangan :

d = Ratio R/X_L

Q = Ratio X_L/R

R = Nilai resistansi pada resistor (Ω)

X_L = Nilai reaktansi kapasitif pada induktor (Ω)

Rumus perhitungan nilai faktor reaktansi dan faktor daya :

Keterangan :
Sin φ = Faktor reaktansi
V_BL = Tegangan drop pada induktor (V)
cos φ = Faktor daya
V_W = Tegangan drop pada resistor (V)
V = Tegangan sumber (V)

Rangkaian Seri Resistor dengan Kapasitor pada Arus Listrik Bolak-Balik 1 Fasa

Gambar rangkaian seri resistor dan induktor dengan sumber arus listrik bolak-balik

Resistor yang dirangkai secara seri dengan kapasitor yang dialiri  arus bolak-balik akan menghasilkan beban impedansi (Z). Impedansi tersebut disebabkan oleh adanya komponen resistor yang menghasilkan beban berupa resistansi (R) dan kapaistor yang menghasilkan beban berupa reaktansi kapasitif  (X_C). Sumber arus listrik bolak-balik atau sumber tegangan bolak-balik ketika dihubungkan secara seri dengan dengan beban resistor dan kapasitor akan mengalirkan arus listrik (I) maka pada resisitor terjadi drop tegangan V_W dan drop tegangan pada kapasitor V_BC.

Gambar segitiga tegangan pada rangkaian seri resistor dan kapasitor

Drop tegangan pada resistor (V_W) digambarkan dengan posisi horizontal (arus se fasa dengan tegangan pada resistor). Drop tegangan pada kapasitor (V_BC) digambarkan tegak lurus dengan garis V_W  berbeda sudut fasa sebesar 90^o. Sumber tegangan (V) merupakan hasil dari penjumlahan secara vektor tegangan V_W dan V_BC. Rumus tegangan pada rangkaian seri resistor dan kapasitor pada arus bolak-balik :

Keterangan :
V = Tegangan sumber (V)
VW = Tegangan drop pada resistor (V)
VBC = Tegangan drop pada kapasitor (V)

Impedansi yang dihasilkan pada rangkaian seri resistor dan kapaistor pada arus bolak-balik dapat diketahui dengan mengetahui nilai reaktansi kapasitif (X_C) pada kapasitor dakam rangkaian tersebut dengan mengunakan rumus berikut :

Keterangan :
X_C = Reaktansi Kapasitif (Ω)
ƒ = Frekuensi (Hz)
C = Nilai kapasitas pada kapasitor (F)
π = 22/7 atau 3,14

Apabila nilai reaktansi kapasitif (X_C) telah diketahui selanjutnya dapat untuk menghitung nilai impedansi (Z) pada rangkaian seri resistor dan kapasitor dengan mengunakan rumus berikut :

Keterangan :
Z = Nilai impedansi pada rangkaian (Ω)
R = niai hambatan atau resistansi pada resistor (Ω)
X_C = Nilai Reaktansi kapasitif (Ω)

Contoh soal rangkaian seri resistor dan kapasitor:

Rangkaian seri kapasitor dengan nilai kapasitas 4 μF dengan resistor yang memiliki nilai hambatan 1 KΩ dirangkai dengan sumber tegangan yang memiliki nilai frekuensi 50 Hz, Berapakah nilai impedansi pada rangkaian tersebut?

Gambar rangkaian

Diketahui : C = 4μF = 4 x10^-6 F
                   R =1 KΩ = 1000 Ω
                   ƒ = 50 Hz
Ditanya    : Z = ?
Jawab       :
Langkah pertama menghitung nilai reaktansi kapasitif (XC) pada kapasitor :

Jika reaktansi kapasitif telah diketahui, selanjutnya menghitung nilai impedansi (Z) pada rangkaian seri resistor dan kapasitor :